Práctica 1

Resumen

Aplicación para crear tu propio problema de 8-puzzle a partir de la solución correcta. Posee una inteligencia artificial capaz de resolverlo y mostrar al usuario el procedimiento para su resolución.

Problema a resolver

El Puzzle deslizante (Sliding-Puzzle en Inglés) o 8-puzzle en su versión 3x3 es un rompecabezas inventado y popularizado por Noyes Palmer Chapman en la década de 1870. Se juega en una cuadrícula de 3 por 3 con 8 bloques cuadrados etiquetados del 1 al 8 y un cuadrado en blanco. Tu objetivo es reorganizar los bloques para que estén en orden. En nuestro caso la solución correcta y la que dará la aplicación por buena será:

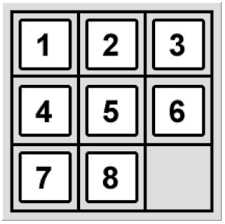
Para resolver el puzzle solo podrás mover las fichas adyacentes (arriba, abajo, derecha e izquierda) a la posición vacía. Al mover una ficha esta ocupará la posición vacía y la posición desde que se ha desplazado pasará a ser la nueva posición vacía. A continuación, se muestra una secuencia de movimientos legales desde un estado inicial (izquierda) hasta el estado resuelto (derecha).

1 3 0 => 1 0 3 => 1 2 3 => 1 2 3 => 1 2 3
4 2 5 => 4 2 5 => 4 0 5 => 4 5 0 => 4 5 6
7 8 6 => 7 8 6 => 7 8 6 => 7 8 6 => 7 8 0

Métodos de resolución

La aplicación puede resolver el rompecabezas con 2 algoritmos diferentes:

Hamming

Definimos el estado del juego como la posición del tablero y el número de movimientos realizados para llegar a la posición del tablero. Partiendo del estado inicial como estado actual del tablero, calculamos los posibles estados a los que se podría llegar. Calculamos los costes de los posibles estados y los comparamos con el coste del estado actual. Si el coste de uno de los estados calculados supera al coste del estado actual descartamos pasar a ese estado y en caso contrario dicho estado pasará a ser el estado actual. Este proceso se repetirá hasta que el estado actual sea la solución correcta. El cálculo del coste se hace sumando la cantidad de bloques en la posición incorrecta, más el número de movimientos realizados hasta el momento para llegar al estado.

Manhattan

Definimos el estado del juego como la posición del tablero y el número de movimientos realizados para llegar a la posición del tablero. Partiendo del estado inicial como estado actual del tablero, calculamos los posibles estados a los que se podría llegar. Calculamos los costes de los posibles estados y los comparamos con el coste del estado actual. Si el coste del estado actual es menor que el de un posible estado hacemos que ese posible estado pase a ser el estado actual y en caso contrario descartamos ese posible estado. Esto lo repetiremos hasta que el estado actual sea la solución correcta. El coste se calcula con la suma de las distancias (suma de la distancia vertical y horizontal) desde los bloques hasta sus posiciones de objetivo, más el número de movimientos realizados hasta el momento para llegar al estado.

Herramientas utilizadas

Unity: motor de la aplicación

Monodevelop: Entorno de desarrollo

C#: lenguaje de programación

Implementación

LogicaFicha: componente de cada ficha de la matriz

Vector2 position: posición lógica de la ficha dentro de la matriz.

int valor: número que sirvepara identificar cada ficha.

TriToMove(): llama a Traslada() si puede la ficha puede ser movida.

CanMove():indica si la ficha puede ser movida.

Traslada(): cambia la ficha visualmente y llama a Swap() del GameManager.

GameManager: gestiona y realiza los movimientos de la matriz y lee el input de teclado:

GameObject [,] tablero:matriz principal del juego

int [,] tableroOriginal: matriz en la que guardamos la solución correcta.

int [,] tableroInt: matriz auxiliar que se pasa a los métodos resolutores de los rompecabezas.

Start(): rellenamos las matrices.

Update(): leemos input de teclado.

Swap(): cambiamos de posición las fichas a nivel lógico en la matriz tablero.

rellenaTableroEnteros(): rellena tableroInt.

rellenarTabero(): rellena tablero.

rellenarTableroOriginal(): rellena tableroOriginal.

resolver(): recibe la solución de los algoritmos y mueve las fichas de tablero para hacerla visible.

dameFicha(): utilizado por resolver() y devuelve la posición lógica de una ficha a través de haberle pasado su valor.

Hamming: Implementa el algoritmo Hamming Priority Function.

int [,] originalPositionBlocks:matriz en la que guardamos la solución correcta.

Struct State: Estado del tablero.

public int [,] blocks: guarda el estado del tablero.

Vector2 emptyBlockPos: guarda la posición de la casilla vacía.

calculateCost(): calcula el coste del estado.

findEmpty(): actualiza emptyBlockPos.

swap(): intercambia los valores de blocks.

State(): constructora del struct State.

ResolveHamming(): gestiona el bucle principal del algoritmo.

isSolved(): te dice si el estado ya es la solución correcta.

resuelve(): actuliza el estado actual.

rellenarTableroOriginal(): rellena originalPositionBocks.

Manhattan: Implementa el algoritmo Manhattan Priority Function.

int [,] originalPositionBlocks:matriz en la que guardamos la solución correcta.

Struct State: Estado del tablero.

public int [,] blocks: guarda el estado del tablero.

Vector2 emptyBlockPos: guarda la posición de la casilla vacía.

calculateCost(): calcula el coste del estado.

findEmpty(): actualiza emptyBlockPos.

swap(): intercambia los valores de blocks.

State(): constructora del struct State.

ResolveHamming(): gestiona el bucle principal del algoritmo.

isSolved(): te dice si el estado ya es la solución correcta.

resuelve(): actuliza el estado actual.

rellenarTableroOriginal(): rellena originalPositionBocks.

Resultados obtenidos

Resuelve los rompecabezas de manera rápida, pero sorprende el gran número de nodos y el coste computacional que requieren los algoritmos. Esto hace que con problemas con un alto número de movimiento pueda llegar a ser menos eficiente, esto se debe a que Unity no es capaz de procesar toda la información y soportar todo el coste computacional.

Objetivos completados

Aplicación perfectamente funcional que permite la creación de un 8-puzzle 3x3 con solución. Implementación de 2 algoritmos eficientes de resolución del rompecabezas, los cuales son Manhattan priority function y Hamming Priority Function.

Objetivos incompletados

No hemos sido capaces generalizar la aplicación. Teníamos la estructura montada pero no hemos conseguido enlazarla con los algoritmos debido a la falta de tiempo.

Dificultades

En la implementación de los algoritmos tuvimos problemas y perdimos mucho tiempo debido a mezclar la parte lógica del algoritmo con la parte visual de Unity. Esto hacía que fuera ineficiente y no funcionase debido al funcionamiento interno de Unity, el cual funciona con referencias y no con copias profundas. Por lo que otro problema fue la utilización de las herramientas debido a nuestro no muy alto conocimiento de ellas.

Otro inconveniente fue la pérdida de tiempo en intentar unir los algoritmos con nuestra estructura para generalizar los puzzles, lo cual al final no conseguimos hacer.